Размер и «ценность» сети
Социальные сети вызывают интерес у исследователей, в частности в связи с тем, что в них возникают качественно новые (по сравнению с набором невзаимодействующих агентов) свойства поведения агентов. Например, в настоящее время идет активная дискуссия вокруг такого понятия, как ценность (value, utility) социальной сети. Это понятие можно перевести, кроме того, как важность, полезность, выгодность, но ниже будет использоваться именно термин «ценность социальной сети».
Ценность социальной сети — это потенциальная доступность агентов, с которыми любой агент может «связаться» в случае необходимости. Эта ценность имеет вполне определенную величину. Так, если рассмотреть американский рынок телефонов, которые могут набирать только номер 911, то покупатели таких телефонов платят за предоставленную возможность связаться со службой спасения, хотя этой возможностью могут никогда и не воспользоваться. Если в данном случае связь даже с одним агентом имеет ценность (которая определяется ценой, уплаченной за купленные телефоны), то потенциальная связь со многими агентами должна иметь, по-видимому, намного большую полезность.
Наверное, одним из первых на ценность социальной сети обратил внимание основатель американской Национальной Радиовещательной Компании (NBC) Давид Сарнов. Закон Сарнова (Sarnoff’s Law) гласит, что ценность радио- или телевещательной сети растет пропорционально количеству зрителей n.
С развитием локальных компьютерных сетей один из авторов технологии Ethernet, Роберт Меткалф, определил (Metcalfe’s Law), что ценность социальной сети асимптотически растет как n2. Обоснование этому закону следующее: каждый агент социальной сети может быть соединен с n-1 остальными агентами, и, таким образом, ценность для него пропорциональна n-1. В сети всего n агентов, поэтому ценность всей сети пропорциональна n(n-1).
Появление Интернета внесло коррективы в оценку роста ценности социальной сети. Давид Рид в своей работе, допуская правильность предыдущих двух законов, добавил (Reed’s Law) в выражение для ценности социальной сети еще одну составляющую, связанную с объединением многих пользователей Интернета в группы. Эта составляющая равна 2n-n-1 и определяется как число подмножеств (групп) множества из n агентов за исключением одиночных элементов и пустого множества. Добавляя к каждому из законов свой коэффициент пропорциональности a, b или с, получаем следующее выражение для ценности социальной сети с большим количеством агентов n: an + bn2 + c2n.
В конце 90-х годов прошлого века произошло массовое разорение ориентированных на Интернет-технологии компаний (так называемых dot-com companies), что заставило исследователей более осторожно отнестись к вопросу о ценности социальных сетей. В некоторых работах приводится критика законов Меткалфа и Рида и предлагается оценивать рост ценности как n ln(n). Главный аргумент в пользу этого закона (который называется законом Ципфа — Zipf’s Law) состоит в том, что в нем, в отличие от первых трех законов, ранжируются ценности связей. Так, если для произвольного агента социальной сети, состоящей из n членов, связи с остальными n-1 агентами имеют ценности от 1 до 1/(n-1), то вклад этого агента в общую ценность сети составляет (для больших n) 1+1/2+ … +1/(n-1)≈ln(n)
Про суммировав по всем агентам, получим полную ценность социальной сети порядка n ln(n). В рамках изложенной аргументации возникает много вопросов. Почему, например, ценности связей распределяются «равномерно» между другими агентами, а не по какому-либо другому принципу? И т. д.
Все приведенные законы, кроме, быть может, закона Сарнова, подвергаются критике, и на сегодняшний день исследователи не пришли еще к единому мнению. По-видимому, эти дискуссии продлятся достаточно долго, так как трудно сформулировать непротиворечивое правило, объясняющее явление в максимальной степени общности и не обращающее внимания на многочисленные детали.
Прибавим еще одно критическое замечание ко всем законам ценности социальных сетей. Очевидно, что ценность двух изолированных социальных сетей должна быть равна сумме ценностей каждой из них, так как из-за отсутствия связей между последними дополнительной ценности не возникает. Такую аддитивность приведенные законы не описывают.
Для ценности социальной сети можно предложить еще одно, вероятностное, описание, которое отражает указанное свойство аддитивности. Ценность социальной сети как величина, зависящая от потенциальных связей всех агентов, очевидно должна возрастать с увеличением количества возможных конфигураций (потенциальных возможностей) этих связей в сети. Действительно, как видно из примера рынка телефонов, который приведен выше, увеличение количества потенциальных возможностей связей в случае необходимости повышает ценность сети. Обозначим через m Ε N количество этих возможных конфигураций, а через ƒ: N → R — ценность сети (где N и R — соответственно множество натуральных и действительных чисел). Тогда свойство монотонности — неубывания ценности с возрастанием количества возможных конфигураций — можно записать в виде ƒ{m1)≥ƒ(m2) для всех m1≥m2.
Рассмотрим две изолированные социальные сети, т. е. такие сети, что любой агент из одной из них не связан ни с каким из агентов другой. Тогда ценность объединения этих двух сетей будет равна сумме ценностей каждой из них. Так как количество возможных конфигураций объединения двух сетей равно произведению m1m2, где m1 и m2 — количества конфигураций первой и второй сетей соответственно, то для ценности изолированных социальных сетей должно быть справедливо свойство аддитивности: ƒ(m1m2) = ƒ(m1) + ƒ{m 2).
Если существует только одна конфигурация связей агентов, то ценность такой социальной сети примем равной нулю, так как эта социальная сеть не дает возможности агентам установить другие потенциальные связи. Поэтому можно ввести свойство нормировки: ƒ(1) = 0.
В теории вероятностей доказано, что функция, удовлетворяющая последним трем свойствам, пропорциональна ln(m), где m — число конфигураций, и носит название энтропии. Если считать, что каждая конфигурация равновероятна, то существует априорная неопределенность, численно равная энтропии ln(m) от числа конфигураций. Так как каждая конкретная конфигурация устраняет неопределенность о связях в сети, то энтропия (апостериорная) каждой конкретной конфигурации становится равной нулю. Смысл ценности социальной сети в приводимой интерпретации состоит в том, что она показывает, насколько в сети может быть полностью устранена априорная неопределенность. Иными словами, осуществляется потенциальная доступность агентов в смысле введенного первоначально определения ценности.
Пусть сеть состоит из n агентов. Перенумеруем всех агентов сети и предположим, что конфигурация сети определяется тем, какой агент от какого получает информацию. Например, агент 1 получает информацию от агента 2, агент 2 получает от агента 3 и т.д. Агент n получает информацию от агента 1. Остальные конфигурации получаются перестановками агентов в описанной исходной конфигурации (кольце). Легко показать, что существует m=п! таких конфигураций сети. Воспользовавшись упрощенной формулой Стирлинга, можно показать, что для большого количества агентов n ценность (в смысле энтропии) социальной сети равна ln(n!) ≈ n ln(n)-n.
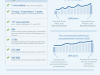
Таким образом, мы получили закон еще более умеренного роста ценности сети по сравнению с законом Ципфа — n ln(n). Например, для сети Facebook, численность членов которой недавно достигла 300 000 000 пользователей, различие между приведенным законом и законом Ципфа составляет около 13%. Для меньших сетей это различие будет увеличиваться.
Что же касается практической реализации, то в настоящее время определился целый класс социальных сетей, существующих в Интернете, которые объединены единой технологией Web 2.0.
Web 2.0, по определению О’Рейли, — методика проектирования систем, которые путем учета сетевых взаимодействий становятся тем лучше, чем больше людей ими пользуются. Особенностью Web 2.0 является принцип привлечения многих пользователей к наполнению и многократной выверке содержания (контента).
В этом определении, как и в приведенных выше законах, существенным фактором является большое количество агентов (современные социальные сети могут охватывать десятки миллионов пользователей), взаимодействие которых в сети увеличивает ее ценность. Исходя из этого, целесообразно использовать развитый аппарат статистической физики и теории информации, который позволяет описывать поведение больших систем на языке теории вероятностей.
Примем, что поведение агента в социальной сети может зависеть от следующих факторов (см рисунок):
- индивидуального — внутренней склонности (предпочтений) агента выбрать то или иное действие в отсутствие какого бы то ни было внешнего влияния;
- социального — определяемого взаимодействием (взаимовлияниями) с другими агентами сети;
- административного — результата воздействия (влияния) на него (управлением) со стороны управляющего органа — центра.
Агентов, которые подвержены описанным факторам, будем называть зависимыми (от одного или нескольких из этих факторов). Если на агентов действует как минимум социальный фактор, то объединяющую их сеть будем называть невырожденной социальной сетью. Не подверженных перечисленным факторам агентов будем называть независимыми. Если у агентов отсутствует зависимость от социального фактора, то такую сеть, состоящую из невзаимодействующих агентов, будем называть вырожденной социальной сетью.
Проводя условно аналогии с моделями термодинамики и статистической физики, можно сказать, что вырожденная социальная сеть с независимыми агентами соответствует идеальному газу. Вырожденная социальная сеть с зависимыми агентами соответствует многоатомному газу. Невырожденная социальная сеть соответствует другим веществам, где присутствует взаимодействие между частицами (взаимовлияние между агентами). Сеть с управлением и без него соответствует наличию или отсутствию воздействия, например, внешнего поля (влияние центра).
Для теории информации можно привести следующие сопоставления. Вырожденной социальной сети соответствует кодирование сообщения без штрафов, а невырожденной социальной сети — кодирование со штрафами. Неаддитивные штрафы соответствуют взаимовлиянию между агентами, аддитивные — влиянию центра.